[코드리뷰] Mip-NeRF Code Breakdown

* 해당 포스팅은 카카오에서 pytorch 코드로 구현한 Mip-NeRF 코드를 기반으로 합니다.

▶ Mip-NeRF 논문 리뷰: 2023.07.23 - [Papers] - [논문리뷰] Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields

[논문리뷰] Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields

▶ NeRF 코드 리뷰: 2023.07.03 - [NeRF] - [코드리뷰] NeRF Code Breakdown

[코드리뷰] NeRF Code Breakdown

---

본 포스팅에서는 NeRF 코드와 상이한 부분만 리뷰하겠습니다.

 

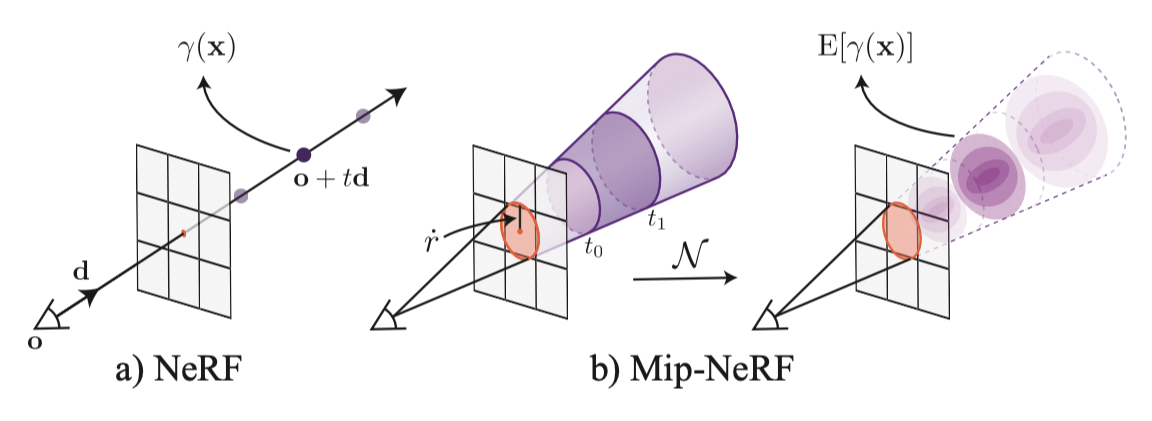
1. Cone tracing - Sampling
2. Integrated positional encoding (IPE)

 

Cone Tracing

기존 NeRF에서 ray를 따라 sampling 했던 것과는 달리, Mip-NeRF는 cone(원뿔)을 캐스팅한 후 이를 일정 간격의 볼륨 (conical frustrum) 으로 sampling (cone tracing) 하고 있다. 

1. Casting Cone

$\mu_{t}, \sigma^{2}_{t}, \sigma^{2}_{r}$ 값을 활용하여 Multivariate Gaussian을 구하는 과정이다. 여기서 Multivariate Gaussian은 conical frustrum 내부 볼륨의 특성을 의미한다.

def cast_rays(t_vals, origins, directions, radii, ray_shape):
    t0 = t_vals[..., :-1]
    t1 = t_vals[..., 1:]
    if ray_shape == "cone":
        gaussian_fn = conical_frustum_to_gaussian
    elif ray_shape == "cylinder":
        gaussian_fn = cylinder_to_gaussian
    else:
        assert False
    means, covs = gaussian_fn(directions, t0, t1, radii)
    means = means + origins[..., None, :]
    return means, covs

1-1) Conical Frustrum

두개의 $t$ 값 사이의 conical frustrum에 위치한 $x$의 집합은 아래와 같다. $$F(x, o, d, \dot{r}, t_{0}, t_{1}) = \left\{ \left( t_{0} < \frac{d^{T} (x-o)}{\lVert d \rVert^{2}_{2}} < t_{1} \right) \wedge \left( \frac{d^{T} (x-o)}{\lVert d \rVert_{2} \lVert x-o \rVert_{2}} > \frac{1}{\sqrt{1 + {(\dot{r} / \lVert d \rVert_{2})}^{2}}} \right) \right\}$$ 만약 $x$가 $(x, o, d, \dot{r}, t_{0}, t_{1})$로 정의된 conical frustrum 안에 위치해 있다면, $F(x, \cdot ) = 1$이다. Conical frustrum 내부의 모든 좌표에 대해 PE를 계산하면, $$\gamma^* (o, t, \dot{r}, t_{0}, t_{1}) = \frac{\int \gamma (x) F(x, o, d, \dot{r}, t_{0}, t_{1})dx}{\int F(x, o, d, \dot{r}, t_{0}, t_{1}) dx}$$ Gaussian을 구하기 위해 $\mu_{t}, \sigma^{2}_{t}, \sigma^{2}_{r}$ 값을 구한다.

def conical_frustum_to_gaussian(d, t0, t1, radius):

    mu = (t0 + t1) / 2 # 중심점
    delta = (t1 - t0) / 2 # 너비의 절반
    t_mean = mu + (2 * mu * delta**2) / (3 * mu**2 + delta**2) # Ray의 평균 거리
    t_var = (delta**2) / 3 - (4 / 15) * (
        (delta**4 * (12 * mu**2 - delta**2)) / (3 * mu**2 + delta**2) ** 2
    ) # Ray의 분산
    r_var = radius**2 * (
        (mu**2) / 4
        + (5 / 12) * delta**2
        - 4 / 15 * (delta**4) / (3 * mu**2 + delta**2)
    ) # Ray의 수직분산

    return translate_gaussian(d, t_mean, t_var, r_var)

• 중심점: $t_{\mu} = (t_{0} + t_{1}) / 2$
• 너비의 절반: $t_{\delta} = (t_{1} - t_{0}) / 2$ * Interval (Critical for numerical stability)
• Ray의 평균 거리: $\mu_{t} = \mu + \frac{2 * \mu * t_{\delta}^{2}}{3 * \mu^{2} + t_{\delta}^{2}}$
• Ray 분산: $\sigma^{2}_{t} = \frac{t_{\delta}^{2}}{3} - \frac{4}{15} * \frac{t_{\delta}^{4} * (12 * \mu^{2} - t_{\delta}^{2})}{{(3 * \mu^{2} + t_{\delta}^{2})}^{2}}$
• Ray의 수직 분산 (Variance perpendicular): $\sigma^{2}_{r} = \dot{r}^{2} * (\frac{\mu^{2}}{4} + \frac{5}{12} * t_{\delta}^{2} - \frac{4}{15} * \frac{t_{\delta}^{4}}{3 * \mu^{2} + t_{\delta}^{2}})$ 

1-2) Cylinder

def cylinder_to_gaussian(d, t0, t1, radius):

    t_mean = (t0 + t1) / 2
    r_var = radius**2 / 4
    t_var = (t1 - t0) ** 2 / 12

    return translate_gaussian(d, t_mean, t_var, r_var)

2) Translate to Gaussian

Conical frustrum 의 좌표계 상의 Gaussian 을 World 좌표계로 변환하는 과정 $$\mu = o + \mu_{t} d, \quad \sum=\sigma_{t}^{2}(dd^{T}) + \sigma_{r}^{2}\left( I - \frac{dd^{T}}{\lVert d \rVert_{2}^{2}} \right)$$ 

* 아래 코드는 카카오 구현에서 lift_gaussian(.) 함수로 정의되어 있지만, 논문의 gaussian lifting 의미와 상이하여 임의로 함수이름을 고쳤습니다.

def translate_gaussian(d, t_mean, t_var, r_var):

    mean = d[..., None, :] * t_mean[..., None]

    d_mag_sq = torch.sum(d**2, dim=-1, keepdim=True)
    thresholds = torch.ones_like(d_mag_sq) * 1e-10
    d_mag_sq = torch.fmax(d_mag_sq, thresholds) # 나누어 주는 값이기 때문에 최솟값을 0이 아닌 1e-10으로 고정

    d_outer_diag = d**2
    null_outer_diag = 1 - d_outer_diag / d_mag_sq
    t_cov_diag = t_var[..., None] * d_outer_diag[..., None, :]
    xy_cov_diag = r_var[..., None] * null_outer_diag[..., None, :]
    cov_diag = t_cov_diag + xy_cov_diag

    return mean, cov_diag

• $\mu = o + \mu_{t} d$
• d_mag_sq: $\lVert d \rVert^{2}_{2}$
• d_outer_diag: $dd^{T}$
• null_outer_diag: $I - \frac{dd^{T}}{\lVert d \rVert_{2}^{2}}$
• t_cov_diag: $\sigma^{2}_{t} (dd^{T})$
• xy_cov_diag: $\sigma^{2}_{r} \left( I - \frac{dd^{T}}{\lVert d \rVert_{2}^{2}} \right)$
• cov_diag: $\sum$

2. Sampling

def sample_along_rays(
    rays_o,
    rays_d,
    radii,
    num_samples,
    near,
    far,
    randomized,
    lindisp,
    ray_shape,
):
    bsz = rays_o.shape[0]
    t_vals = torch.linspace(0.0, 1.0, num_samples + 1, device=rays_o.device)
    if lindisp:
        t_vals = 1.0 / (1.0 / near * (1.0 - t_vals) + 1.0 / far * t_vals)
    else:
        t_vals = near * (1.0 - t_vals) + far * t_vals

    if randomized:
        mids = 0.5 * (t_vals[..., 1:] + t_vals[..., :-1])
        upper = torch.cat([mids, t_vals[..., -1:]], -1)
        lower = torch.cat([t_vals[..., :1], mids], -1)
        t_rand = torch.rand((bsz, num_samples + 1), device=rays_o.device)
        t_vals = lower + (upper - lower) * t_rand
    else:
        t_vals = torch.broadcast_to(t_vals, (bsz, num_samples + 1))

    means, covs = cast_rays(t_vals, rays_o, rays_d, radii, ray_shape)

    return t_vals, (means, covs)

Integrated Positional Encoding

IPE 는 Cone tracing으로 샘플링된 Multivariate Gaussian을 통해 연산된다.

t_vals, samples = sample_along_rays(
    rays_o,
    rays_d,
    radius,
    num_samples,
    near,
    far,
    randomized,
    lindisp,
    ray_shape,
)

samples_enc = integrated_pos_enc(samples, 2, 16)

def integrated_pos_enc(samples, min_deg=0, max_deg=16):
	scales, shape = pe_fourier(samples, min_deg, max_deg)
	y, y_var = lift_gaussian(samples, scales, shape)
	samples_enc = expected_sin(
        torch.cat([y, y + 0.5 * np.pi], axis=-1), torch.cat([y_var] * 2, axis=-1))[0]
    
    return samples_enc

1) Rewrite the PE as a Fourier feature

 

$$P=\begin{bmatrix} 1 & 0 & 0 & 2 & 0 & 0 & & 2^{L-1} & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 & ... & 0 & 2^{L-1} & 0 \\ 0 & 0 & 1 & 0 & 0 & 2 & & 0 & 0 & 2^{L-1} \end{bmatrix}^{T} , \quad \gamma (x)=\begin{bmatrix} sin(Px) \\ cos(Px) \end{bmatrix}$$

def pe_fourier(samples, min_deg=0, max_deg=16):
    x, x_cov_diag = samples
    scales = torch.tensor([2**i for i in range(min_deg, max_deg)]).type_as(x)
    shape = list(x.shape[:-1]) + [-1]
    
    return scales, shape

2) Lift the multivariate Gaussian

$$\mu_{\gamma} = P\mu ,\quad \sum_{\gamma} = P\sum P^{T}$$

def lift_gaussian(samples, scales, shape):
    x, x_cov_diag = samples
    y = torch.reshape(x[..., None, :] * scales[:, None], shape)
    y_var = torch.reshape(x_cov_diag[..., None, :] * scales[:, None] ** 2, shape)

    return y, y_var

3) Expectations over lifted multivariate Gaussian

$$\mathsf{E}_{x \sim \mathcal{N}(\mu, \sigma^{2})}[sin(x)] = sin(\mu) exp \left( -(1/2)\sigma^{2} \right)$$ $$\mathsf{E}_{x \sim \mathcal{N}(\mu, \sigma^{2})}[cos(x)] = cos(\mu) exp \left( - (1/2) \sigma^{2} \right)$$

def expected_sin(x, x_var):
    y = torch.exp(-0.5 * x_var) * torch.sin(x)
    y_var = 0.5 * (1 - torch.exp(-2 * x_var) * torch.cos(2 * x)) - y**2
    y_var = torch.fmax(torch.zeros_like(y_var), y_var)
    return y, y_var